между этими двумя состояниями; определение первой цифры реализует эту подцель. Теперь текущее
состояние включает знание первой цифры. Разрыв между текущим и целевым состоянием все еще
существует, и его можно уменьшить, определив вторую цифру, и так далее. Итак, главная идея
сокращения разрыва состоит в установлении подцелей, достижение каждой из которых переводит нас в
состояние, более близкое к нашей цели.
Сходная, но более сложная стратегия называется «анализ средства и результата». В ней текущее
состояние сравнивается с целевым состоянием, чтобы найти наиболее важное различие между ними;
устранение этого различия становится главной подцелью. Затем ведется поиск средства или процедуры
для достижения этой подцели. Если такая процедура найдена, но оказывается, что что-то в текущем
состоянии не дает ее применить, вводится новая подцель по устранению этого препятствия. Эта
стратегия применяется во многих случаях решения задач на основе здравого смысла. Вот пример:
«Я хочу отвести своего сына в детский сад. Каковы [наиболее важные] различия между тем, что
я имею, и тем, что хочу? Одно из них — расстояние. Что [какая процедура] изменяет расстояние? Мой
автомобиль. Мой автомобиль не работает. Что нужно, чтобы он заработал? Новый аккумулятор. Где
есть новый аккумулятор? В автомастерской» (Newell & Simon, 1972; цит. по: Anderson, 1990, р. 232).
Анализ средства и результата — более сложная стратегия по сравнению с сокращением разрыва,
поскольку он позволяет предпринять действие, даже если оно приводит ко временному уменьшению
сходства между текущим и целевым состоянием. В вышеприведенном примере автомастерская может
находиться в противоположном направлении от детского сада. Так что, отправляясь в мастерскую, вы
тем самым временно увеличиваете расстояние до цели, и все же этот шаг существен для решения
задачи.
Еще одна стратегия — это действие, в котором происходит обратное движение от цели. Она
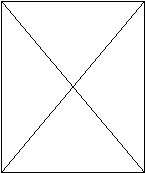
особенно полезна при решении математических задач, пример одной из которых показан на рис. 9.12.
Задача такая: зная, что ABCD — прямоугольник, доказать, что диагонали AD и ВС равны. Мысленно
двигаясь назад, можно рассуждать так:
«Как доказать, что AD и ВС равны? Я мог бы это сделать, если бы доказал, что треугольники
ACD и ВDС равны. Я могу доказать, что треугольники ACD и BDC равны, если докажу, что две
стороны и заключенный между ними угол равны» (взято из: Anderson, 1990, р. 238).
B
D
C
A
Рис. 9.12. Задача из геометрии. Зная, что ABCD — прямоугольник, доказать, что отрезки AD и
ВС имеют одинаковую длину.
Мы рассуждаем, идя от цели к подцели (доказывая равенство треугольников), от этой подцели —
к другой подцели (доказывая, что стороны и угол равны) и так далее, пока мы не подойдем к подцели,
для реализации которой у нас есть готовое средство.
Три рассмотренные нами стратегии — сокращение разрыва, анализ средства и результата и
движение от цели — являются чрезвычайно общими и могут применяться практически к любой задаче.
Эти стратегии, которые часто называют слабыми методами, не основываются ни на каком конкретном
знании и могут быть даже врожденными. Люди могут особенно полагаться на эти слабые методы, когда
они впервые изучают какую-либо область и работают над задачами с незнакомым содержанием. Как мы
скоро убедимся, когда люди получают специальные знания в какой-либо области, они разрабатывают
более мощные предметно-ориентированные методы (и репрезентации), которые начинают преобладать
над слабыми методами (Anderson, 1987).
Представление о задаче

