выходные реакции.
Небольшая сеть, показанная на рис. 3, имеет конфигурацию, позволяющую проиллюстрировать
поведение согласно правилу исключающего ИЛИ. В этой конфигурации вход A
сам по себе не может
активизировать элемент X, т. к. вес связи А — X не превышает величины порога X, однако вход A может
активизировать элемент R, т. к. его порог оказывается достаточно низким для того чтобы связь
A
—
R
оказалась эффективной. Точно так же, вход В может активизировать лишь узел R. Т. о., входы A
и В
могут каждый по отдельности активизировать выход этой сети. Однако, согласно правилу
исключающего ИЛИ, взятые вместе входы А и В будут подавлять выход. Это происходит потому, что
суммарный вес связей входов А и В будет активизировать элемент X, а этот элемент X имеет большую
отрицательную связь с элементом R. Следовательно, совместное появление входов А и В аннулирует их
индивидуальные положительные связи с элементом R.
Автоассоциативные сети
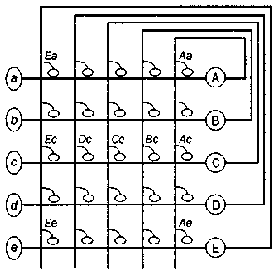
Пример небольшой автоассоциативной сети показан на рис. 4.
Рис. 4. Автоассоциативная сеть, в которой все выходные уровни могут связываться со входными
уровнями
Каждый из пяти элементов (А, В, С, D, Е) получает один внешний вход (a, b, с, d, e). Эти внешние
входы обладают фиксированными связями, каждая из к-рых способна активизировать выход из соотв.
элементов. Кроме того, каждый элемент получает пять возвратных входов, по одному на каждый выход
из элементов, включ. его собственный. Напр., как показано на рис. 4, элемент С имеет пять связей,
обозначенных как Aс,
Bc, Сс, Dc и Еc. Эти связи являются модифицируемыми и функционируют в
соответствии с теми же самыми правилами обучения, что и единственный элемент или многослойная
сеть. Т. о., всякий раз, когда выход и вход являются активными, на их пересечении может возникать
эффективная связь.
Помимо др. вещей, автоассоциативные сети могут реализовывать 3 функции, к-рые
представляют особый интерес для психологии.
1. Завершение паттерна. Если множество взаимосвязей было хорошо определено в
автоассоциативной сети, тогда уже часть исходных входов может восстановить полное множество
выходов. Напр., предположим, что для сети, изображенной на рис. 4, неоднократно предъявлялись
входы а и е. Отсюда следует, что установились бы четыре взаимосвязи, а именно Аа, Ае, Еа и Ее, к-рые
локализованы в четырех углах матрицы пересечений. Впоследствии вход а сам по себе активизировал
бы оба выхода, А и Е, через связи Аа и Ае. Точно так же, вход е активизировал бы оба выхода через
связи Еа и Ее.
2. Помехоустойчивость.
3. Суперпозиционная память. Автоассоциативные сети могут хранить огромное количество
наборов входов. Это свойство позволяет им извлекать как прототипические паттерны, так и
специфические образцы. Напр., Мак-Клелланд и Румельхарт продемонстрировали, что сеть, состоящая
из 24 элементов и 552 потенциальных взаимосвязей, могла бы хранить и надежно извлекать 3
различных прототипических паттерна, каждый из к-рых осн. на 50 различных образцах. Они показали,
что паттерн для по меньшей мере одного конкретного образца тж может быть извлечен, если этой сети
представлено подмножество входов, корреспондирующих с именным признаком (пате tag)
этого

