изменения порядка не
153
являются, по-видимому, неблагоприятными. Важна, вероятно, не величина
отдельного отклонения от первоначального ряда; помогать или мешать ясному
видению целого может скорее определенный тип упорядоченности. В случае
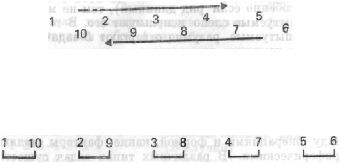
1+10+2+9+3+8+4+7+5+6
испытуемый иногда останавливается и восклицает: «Тут есть
последовательность: эти числа возрастают, а эти — убывают», показывая
Рис. 78
или образует пары:
Рис. 79
Последний прием приближается к хорошо известным приемам «быстрого
счета», которыми пользуются бухгалтеры, складывая большие числа. Вместо
того чтобы считать, последовательно складывая числа, они считают парами
или тройками, образуя легко запоминаемые круглые числа. Этим приемам,
конечно, недостает понимания связи с «принципом» построения ряда.
III
Столкнувшись с задачей определения суммы ряда и не получив никакой
помощи, многие не могут найти гауссова решения. Почему? Что делает эту
задачу для многих столь трудной? Что кроется за словами: «Чтобы решить эту
задачу, нужно обладать гением юного Гаусса»? Но почему тогда это сделал
маленький мальчик из упоминавшихся примеров, причем сделал это
последовательно и с легкостью? Что с психологической точки зрения лежит в
основе таких творческих достижений?
Задачи Гаусса связаны со структурными трудностями. И чтобы преодолеть
эти трудности и, несмотря на них,
154
увидеть путь к решению, требуются некоторые условия. На основании своего
опыта могу сказать, что существенными чертами подлинного решения является
то, что продуктивно мыслящий человек

