величины, как размах. Дисперсия показывает, насколько составляющие распределение величины
отстоят от средней величины этого распределения. Чтобы вычислить дисперсию, сначала подсчитаем
отклонения каждой величины (d) от среднего, вычтя из среднего каждую величину (табл. П3). Затем
надо каждую разницу возвести в квадрат, чтобы не было отрицательных чисел. Наконец, эти
отклонения складываются вместе и делятся на общее количество отклонений, давая в результате
средний квадрат отклонения. Средний квадрат отклонения называется дисперсией. Проделав это с
данными из рис. П3, мы обнаружим, что дисперсия у класса А равна 2,0, а у класса Б — 130. Очевидно,
что у класса Б вариативность показателей значительно сильнее.
Таблица П3. Вычисление дисперсии и стандартного отклонения
Оценки Класса А (Среднее = 75)
d
d²
77-75
2
4
76-75
1
1
75-75
0
0
74-75
-1
1
73-75
-2
4
Сумма d² = 10
Дисперсия = среднее по d² = 10 / 5 = 2,0
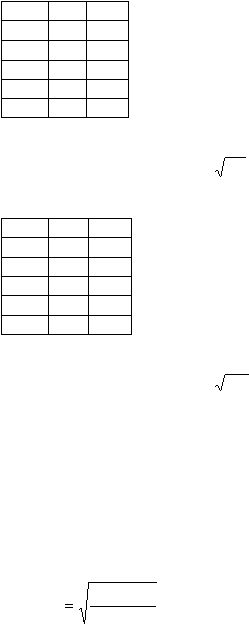
Стандартное отклонение (?) =
0
,
2
= 1,4
Оценки Класса Б (Среднее = 75)
d
d²
90-75
15
225
85-75
10
100
75-75
0
0
65-75
-10
100
60-75
-15
225
Сумма d² = 650
Дисперсия = среднее по d² = 650 / 5 = 130
Стандартное отклонение (?) =
130
= 11,4
Неудобство дисперсии состоит в том, что она выражена в единицах измерения, возведенных в
квадрат. Поэтому величина дисперсии, равная 2
у класса А, не означает, что его усредненные
показатели отличаются от среднего на 2 пункта. Она показывает, что 2 — это результат усреднения
возведенных в квадрат значений, на которые показатели отличаются от среднего. Чтобы получить меру
отклонения, выраженную в первоначальных единицах измерения (в данном случае это количество
единиц, набранных на экзамене), надо просто извлечь из дисперсии квадратный корень. Результат
называют стандартным отклонением. Оно обозначается греческой буквой ? (сигма), используемой
также в некоторых других статистических вычислениях, которые мы обсудим вкратце. Стандартное
отклонение вычисляется по следующей формуле:
N
d
2
сумма
?
Пример вычисления стандартного отклонения. (табл. П3). Показатели выборок из двух
классов представлены в виде, удобном для вычисления стандартного отклонения. На первом этапе
вычитаем среднее из каждого показателя (среднее = 75 в обоих классах). В результате получаем
положительные величины d для показателей, которые больше среднего, и отрицательные для тех,
которые меньше его. Когда полученные величины будут возведены в квадрат, знак минус пропадет
(следующая колонка в табл. П3). Возведенные в квадрат разности складываются и делятся на N —
количество элементов выборки, в нашем случае N = 5. Извлекая квадратный корень, получаем
стандартное отклонение. [В этом ознакомительном изложении мы везде будем использовать ? (сигма).
Однако в научной литературе для обозначения стандартного отклонения выборки используется
маленькая буква s, а через а обозначают стандартное отклонение для всей группы. Кроме того, при
вычислении стандартного отклонения для выборки (s) сумма всех d² делится не на N, а на N-1. В случае

