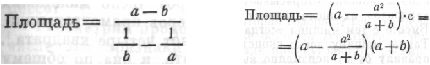
2)
56 = 7 умноженное на сколько? Ответ: 8.
3)
45 = 6 умноженное на сколько?
Предположим, что ученик ответил на третий вопрос: «Семь». И когда вы
спросили его, почему он так думает, он сказал: «Разве это не очевидно?
Четвертая цифра на единицу больше третьей:
1)
12 3 4
2)
56 7 8
3)
45 6 7».
Разве здесь существенно, что ученик основывал свою «гипотезу» на очень
малом числе случаев? Нет. Сама гипотеза нелепа: увеличение чисел в этом
случае не имеет никакого отношения к структуре ситуации, к требованиям
ситуации, к соединению знаком равенства, к смыслу чисел, расположенных
слева, к смыслу знака умножения
56
в правой части. Оно не связано с теми структурными свойствами, которые
обусловливают требования к разумному решению или осмысленной гипотезе.
15. Теперь мы приведем дополнительные примеры диких процедур,
ведущих к правильному ответу. Ошибочным здесь является не отсутствие
доказательства, а то, что ни один из шагов этой процедуры не имеет разумной
связи с заданием.
Как определить площадь прямоугольника:
I
II
1)
а
–
b
2) 1/a
3) 1/b
4) вычтите 2) из 3)
5) разделите 1) на результат,
полученный в 4)
1)
замените a+b на с
2)
а²
3)
разделите 2) на 1)
4)
вычтите 3) из a
5)
умножьте результат на
1)
16. Я выбрал искусственные примеры для того, чтобы объяснить суть дела,
но подобные вещи случаются и без вмешательства психолога.
Ребенок в школе заучивает вместе с сопутствующими упражнениями
формулы для периметра, 2(а+b), и для площади, а ? b, прямоугольника.
Спустя некоторое время ему предлагаются задачи, требующие вычисления
площади прямоугольников в контексте решения более широких задач. Ему
приходит на ум формула 2(а+b), и он ошибочно использует ее, даже не

