66
Поэтому анализ распределения необходим не только при использо-
вании статистических норм, но и в случае абсолютных и критери-
альных норм.
Как известно, частотное распределение суммарных баллов
имеет удобную графическую интерпретацию в виде кривых распре-
делений: гистограммы и кумуляты (см., в частности, удачное попу-
лярное введение в описание распределений в книге: Кимбл Г., 1982,
с. 55-70). В случае гистограммы по оси абсцисс откладываются «сы-
рые очки» -первичные показатели суммарных баллов, возможных
для данного теста, по оси ординат - относительные частоты (или
проценты) встречаемости баллов в выборке стандартизации (Анаста-
зи А., 1982, с. 66). Как известно, для «колоколообразной» кривой
нормального распределения дисперсия визуализируется как пара-
метр, ответственный за «распластанность» графика плотности веро-
ятности (теоретического аналога эмпирической кумуляты) вдоль оси
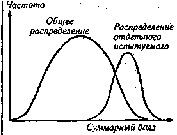
X. Чтобы визуализировать дисперсию ошибки измерения, нужно
было бы многократно провести тест с одним испытуемым и постро-
ить графическое распределение частот его индивидуальных баллов
(рис. 1).
Очевидно, что дифференцирующая способность теста сводит-
ся к нулю, если кривые, иллюстрирующие «истинную» и «ошибоч-
ную» дисперсии» совпадают. Как видим, анализ распределения тес-
товых баллов необходим уже для анализа надежности теста (см. раз-
дел 3.2).
Проблема меры в психометрике и свойства пунктов теста. В
физических измерениях калибровка шкалы производится на основе
контроля за равномерным варьированием измеряемого свойства в
эталонных объектах. Носителем меры является эталон- физический
объект, стабильно сохраняющий заданную величину измеряемого
свойства. В дифференциальной психометрике такие физические эта-
лоны отсутствуют: мы не располагаем индивидами, которые были
бы постоянными носителями заданной величины измеряемого свой-
ства.
Рис. 1.Соотношение индивидуальной и общей вариации
тестовых баллов
Роль косвенных эталонов в психометрике выполняют сами
тесты: в том смысле, в каком трудность задач можно рассматривать

