81
ние С (иногда на это требуются месяцы и годы после момента тести-
рования), психодиагност группирует индивидов по порядку возрас-
тания балла X
i
и для каждого деления исходной шкалы сырых тесто-
вых баллов подсчитывает эмпирическую вероятность Р попадания в
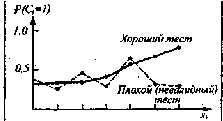
«высокую» группу по критерию С. На рис. 5 показаны распределе-
ния вероятности Р (C
i
= 1) в зависимости от X
i
Рис. 5 Эмпирическая зависимость
между вероятностью
критериального события и тестовым баллом
Очевидно, что кривая на рис. 5 по своей конфигурации может
совершенно не совпадать с кумулятивной кривой распределения
частот появления различных X
i
. Кривая, представленная на рис. 5,
является эмпирической линией регрессии С по X
i
Теперь можно
сформулировать основное требование к критериальному тесту: ли-
ния регрессии должна быть монотонной функцией С от X
i
Иными
словами, ни для одного более высокого значения X. вероятность Р не
должна быть меньшей, чем для какого-либо менее высокого значе-
ния X
i
Если это условие выполняется, то открывается возможность
для критериального шкалирования сырых баллов X. Так же как в
случае с интервальной нормализацией», когда применяется поточеч-
ный перевод интервалов Х в интервалы Z, для которых выполняется
нормальная модель распределения, так и при критериальном шкали-
ровании к делениям сырой шкалы X применяется поточечный пере-
вод прямо в шкалу Р на основании эмпирической линии регрессии.
Например, если испытуемый А получил по тесту X 18 сырых баллов
и этому результату соответствует Р=0,6, то испытуемому А ставится
в соответствие показатель 60 %.
Конечно, любая эмпирическая кривая является лишь прибли-
женной моделью той зависимости, которая могла бы быть воспроиз-
ведена на генеральной совокупности. Обычно предполагается, что
на генеральной совокупности линия регрессии С по Х должна иметь
более сглаженную форму. Поэтому обычно предпринимаются по-
пытки аппроксимировать эмпирическую линию регрессии какой-
либо функциональной зависимостью, что позволяет затем произво-
дить прогноз с применением формулы (а не таблицы или графика).
Например, если линия регрессии имеет вид приблизительно
такой, какой изображен на рис. 6, то применение процентильной

