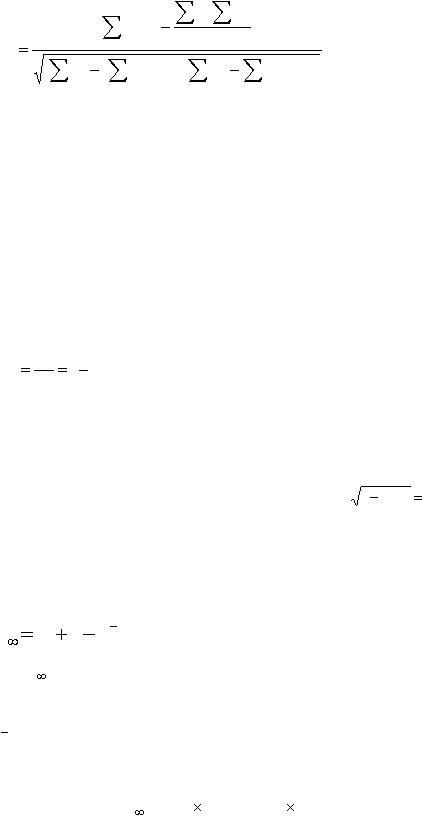
85
пытуемых, обычно через две недели после первого тестирования.
Для интервальных шкал подсчитывается хорошо известный коэф-
фициент корреляции произведения моментов Пирсона:
)
/
)2
)(
/
)
(
(
2i
2
2i
2
1i
2
1i
2i
1i
2i
2
1i
12
n
x
x
n
x
x
n
x
x
x
x
r
где х1
i
. - тестовый балл i-го испытуемого при первом измере-
нии;
х2
i
. - тестовый балл того же испытуемого при повторном изме-
рении;
n
- количество испытуемых.
Оценка значимости этого коэффициента основывается на не-
сколько иной логике, чем это обычно делается при проверке нулевой
гипотезы - о равенстве корреляций нулю. Высокая надежность дос-
тигается тогда, когда дисперсия ошибки оказывается пренебрежи-
тельно малой. 'Относительную долю дисперсии ошибки легко опре-
делить по формуле
12
2
2
2
0
1
r
S
S
S
x
e
(3.2.4)
Таким образом, для нас существеннее близость к единице, а не
отдаленность от нуля. Обычно в тестологической практике редко
удается достичь коэффициентов, превышающих 0,8. При г = 0,75 от-
носительная доля стандартной ошибки равна
5
,
0
75
,
0
1
. Этой
ошибкой, очевидно, нельзя пренебречь. При такой ошибке эмпири-
чески полученное отклонение индивидуального тестового балла от
среднего по выборке оказывается, как правило, завышенным. Для
того чтобы выяснить «истинное» значение тестового балла индиви-
да, применяется формула
x
r)
rx
x
i
1
(
(3.2.5)
где
x
- истинный балл; '
х
i
— эмпирический балл i-го испытуемого;
r
-
эмпирически измеренная надежность теста;
x
- среднее для теста.
Предположим, испытуемый получил балл IQ по шкале Стэн-
форда.-Бине, равный 120 нормализованным очкам, М = 100, г = 0,9.
Тогда истинный балл
x
= 0,9
120 + 0,1
100 =118.
Конечно, требование ретестовой надежности является кор-
ректным лишь по отношению к таким психическим характеристикам
индивидов, которые сами являются устойчивыми во времени. Если

