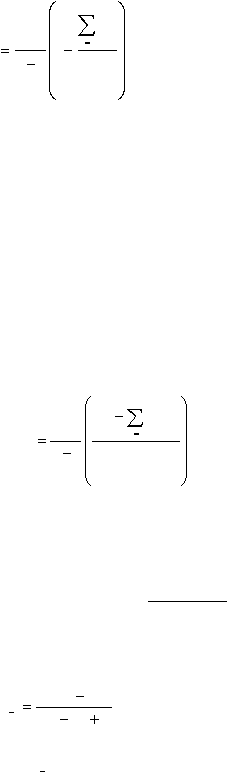
87
2
1
2
1
1
x
j
j
j
S
S
k
k
a
(3.2.8)
где а - коэффициент Кронбаха;
k- количество пунктов теста;
2
j
S
- дисперсия по j-му пункту теста;
2
x
S
- дисперсия суммарных баллов по всему тесту.
Обратите внимание на структурное подобие формулы Кронба-
ха (3.2.2) и формулы Рюлона (3.2.8).
Несколько раньше была получена формула Кьюдера - Ричард-
сона, аналогичная формуле Кронбаха для частного случая - когда
ответы на каждый пункт теста интерпретируются как дихотомиче-
ские переменные с двумя значениями (1 и 0):
2
1
2
20
1
x
k
j
j
j
x
S
q
p
S
k
k
KR
(3.2.9)
где KR
20
- традиционное обозначение получаемого коэффици-
ента;
j
j
q
p
-дисперсия i-и дихотомической переменной, какой являет-
ся
i-й пункт теста; р =
n
верно»
N
)
«
(
, q = 1 - p
В 1957 г. Дж. Ките предложил следующий критерий для оцен-
ки статистической значимости коэффициента a:
a
a)
k(
n
k(
X
n
1
)
1
2
1
(3.2.10)
где
2
1
n
X
- эмпирическое значение статистики % квадрат с п-1
степенью свободы;
k
-
количество пунктов теста;
n
- количество испытуемых;.
a
- надежность.
Формулы (3.2.8) и (3.2.9) позволяют оценить взаимную согла-
сованность пунктов теста, используя при этом только подсчет дис-
персий. Однако коэффициенты а и KR2
I>
позволяют оценить и сред-
нюю корреляцию между i-м и j-м произвольными пунктами теста,

