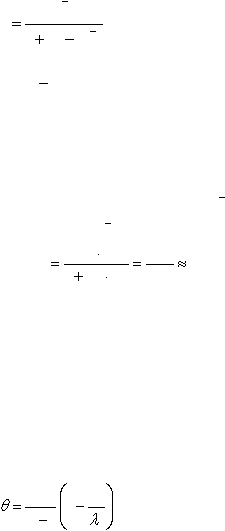
88
так как связаны с этой средней корреляцией следующей формулой:
ij
ij
r
k
r
k
a
)
1
(
1
11)
где
ij
r
-
средняя корреляция между пунктами теста. Легко
увидеть идентичность формулы (3.2.11) обобщенной формуле
Спирмена - Брауна, позволяющей прогнозировать повышения син-
хронной надежности теста с увеличением количества пунктов теста
в k
раз (Аванесов В. С., 1982, с. 121). Из этой формулы видно, что
при больших k
малое значение
ij
r
может сочетаться с высокой на-
дежностью. Пусть
ij
r
= 0,1, a k =100, тогда по формуле (3.2.11)
91
,
0
9
,
10
10
1
,
0
99
1
1
,
0
100
a
Широкое распространение компьютерных программ фактор-
ного анализа для исследования взаимоотношений между пунктами
теста (по одномоментным данным) привело к обоснованию еще од-
ной достаточно эффективной формулы надежности теста, которой
легко воспользоваться, получив стандартную распечатку компью-
терных результатов факторного анализа по методу главных компо-
нент:
1
1
1
1
k
k
(3.2.12)
где ?
- коэффициент, получивший название тета-надежности
теста;
k
-
количество пунктов теста;
?1 - наибольшее значение характеристического корня матрицы
интеркорреляций пунктов (наибольшее собственное значение,
или абсолютный вес первой главной компоненты).
Как и предыдущие формулы, формула (3.2.12) также относит-
ся к оценке надежности теста, направленного на измерение одной
характеристики. Но, кроме того, она применима и для многофактор-
ного теста, хотя и нуждается в пересчете после первоначального от-
бора пунктов, релевантных фактору (после того, как на основании
многофакторного анализа отобраны пункты по одному фактору,
снова проводится факторный анализ - только для этих отобранных
пунктов).
Надежность отдельных пунктов теста. Надежность теста обес-
печивается надежностью пунктов, из которых он состоит. Чтобы по-

