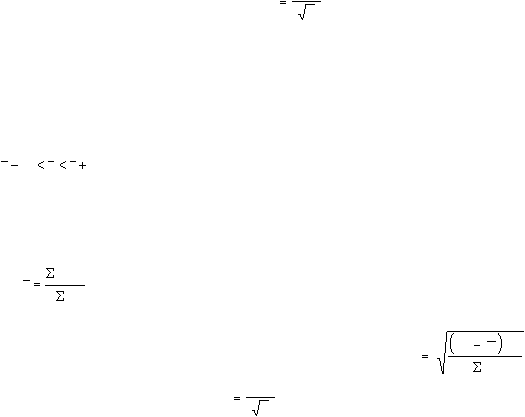
и, как мы знаем, вероятность такого варианта равняется 683 случаям из 1000,
т. е. 0,683. При снижении точности предсказания в два раза, т. е. при t
= 2,
вероятность возрастает до 0,954, при t = 3 — до 0,997, при t = 4 — до 0,999.
Используя коэффициент t, мы можем ввести определение предельной
ошибки выборки ?.
Предельная ошибка выборки непосредственно зависит
от принятого нами уровня точности — коэффициента t. ?= t х
?.
Если мы не
хотим ошибиться в своих заключениях, надо увеличить t, при t
= 4
вероятность того, что выборочная средняя не выйдет за пределы четырех
средних отклонений, составит 0,999.
Расчет средней ошибки выборки, как было показано выше, зависит от
однородности генеральной совокупности — ?
ген
. Новыборка производится
как раз для того, чтобы установить параметры генеральной совокупности.
Поэтому практического смысла формула
n
ген
?
?
не имеет. Вместе с тем, при
достаточно большом числе наблюдений среднее квадратическое отклонение
выборочных средних от общей средней становится равным среднему
квадратическому отклонению генеральной совокупности, т. е. меру вариации
в генеральной совокупности можно заменить мерой вариации в
совокупности выборочной. В данном случае
?
обозначает пределы, в
которых может находиться с определенной вероятностью генеральная
средняя:
?
x
x
t?
x
Рассмотрим частотное распределение выборочной совокупности 807
школьников по количеству имевшихся у них наличных денег (табл. 5.14).
Прежде всего необходимо подсчитать среднюю арифметическую где х
—
значения переменной, р — частоты. Среднее
количество
p
1
p
1
x
x
денег у ребенка составляло тогда 45 руб. Затем надо
выяснить, насколько велика разнородность обследованных по интересующей
нас переменной, т. е. среднее квадратическое отклонение
p
p
2
x
1
x
?
По
формуле средней ошибки выборки
n
ген
?
?
устанавливаем, что она равна 1,3
руб. Далее у нас есть воз
183

