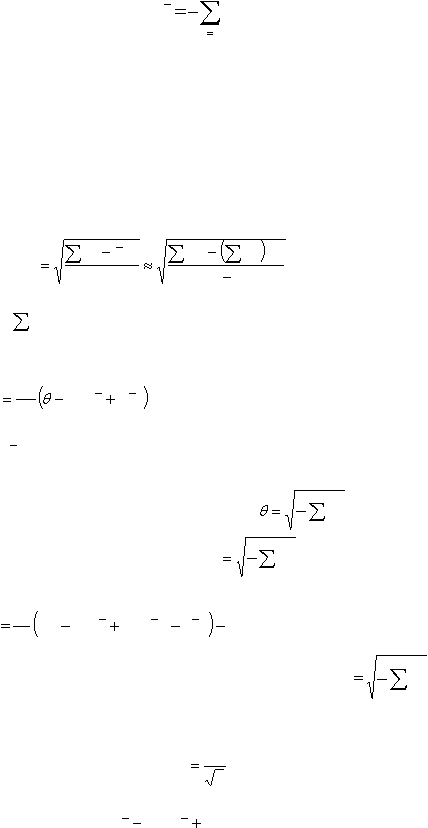
74
n
j
j
j
y
p
n
x
1
1
,
(3.1.1)
где x
j
– балл i-го испытуемого;
y
i
-значение i-го балла по порядку возрастания;
p
i
- частота встречающегося i-го балла;
n
- количество испытуемых в выборке (объем);
m
- количество градаций шкалы (количество баллов).
2.
Среднее квадратическое (стандартное) отклоне-
ние:
3.
1
/
)2
(x
2
2
n
n
x
x
n
x
s
,
(3.1.2)
где
2
x
- сумма квадратов тестовых баллов для и испытуе-
мых.
3. Асимметрия:
3
2
3
2x
3C
1
x
S
AS
(3.1.3)
где
x
- среднее арифметическое значение;
S
- стандартное отклонение;
?
- среднее кубическое значение:
3
3
1
x
n
,
С - среднее квадратическое:
2
1
x
n
C
4. Эксцесс:
3
3x
6C
403
1
4
2
2
4
4
x
x
Q
s
Ex
,
(3.1.4)
где Q - среднее значение четвертой степени:
4
4
1
x
n
Q
.
Стандартная ошибка среднего арифметического значения (ма-
тематического ожидания) оценивается по формуле:
n
s
s
m
(3.1.5)
На основе ошибки математического ожидания строятся дове-
рительные интервалы:
m
m
S
x
S
x
2
;
2
(
)
Если тестовый балл какого-либо испытуемого попадает в гра-
ницы доверительного интервала, то нельзя считать, что испытуемый
обладает повышенным (или пониженным) значением измеряемого
свойства с заданным уровнем статистической значимости.
Асимметрия и эксцесс нормального распределения должны

