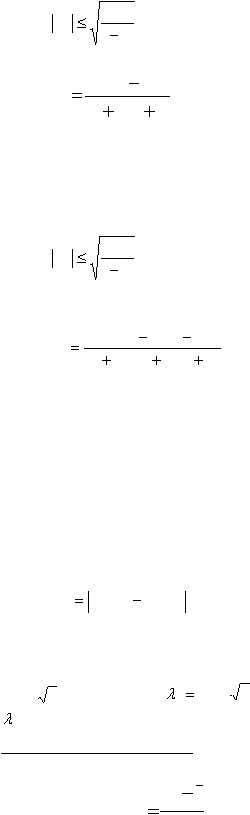
75
быть равны нулю. Если хотя бы один из двух параметров сущест-
венно отличается от нуля, то это означает анормальность получен-
ного эмпирического распределения.
Проверку значимости асимметрии можно произвести на осно-
ве общего неравенства Чебышева:
p
S
As
a
1
(3.1.6)
где S
a
- дисперсия эмпирической оценки асимметрии:
)
3
)(n
1
(n
)
1
(n
6
S
a
,
(3.1.7)
где р -
уровень значимости или вероятность ошибки первого
рода: ошибки в том, что будет принят вывод о незначимости асим-
метрии при наличии значимой асимметрии (в формулу подставляют
стандартные р = 0,05 или р = 0,01 и проверяют выполнение неравен-
ства). Сходным образом оценивается значимость эксцесса:
p
S
Ex
e
1
(3.1.8)
где S
е
- эмпирическая дисперсия оценки эксцесса:
)
5
)(n
3
(n
)
1
(n
)
3
)(n
2
(n
24n
2
S
e
.
(3.1.9)
]
Гипотезы об отсутствии асимметрии и эксцесса принимаются
с вероятностью ошибки р (пренебрежимо малой), если выполняются
неравенства (3.1.6) и (3.1.8).
Более легкий метод проверки нормальности эмпирического
распределения основывается на универсальном критерии Колмого-
рова. Для каждого тестового балла у. (для каждого интервала равно-
значности при дискретизации непрерывной хронометрической шка-
лы) вычисляется величина D. - модуль отклонения эмпирической и
теоретической интегральных функций распределения:
)
(z
)
(
j
j
j
U
y
F
D
(3.1.10)
где F- эмпирическая интегральная функция (значение кумуля-
ты в данной точке у
j
); U
—
теоретическая интегральная функция,
взятая из таблиц¹. Среди D
j
отыскивается максимальное значение
D
max
n
, и величина
n
D
e
max
сравнивается с табличным значением
t
критерия Колмогорова.
1
Значение z
j
определяется после стандартизации шкалы в единицах стандартно-
го отклонения:
S
x
y
z
S
j
j
:

