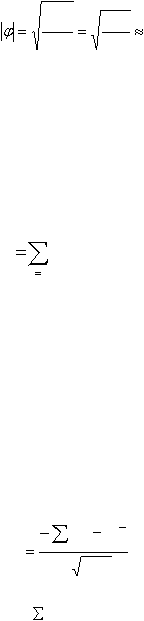
91
распределения тестовых баллов
В некоторых случаях подобный анализ позволяет уточнить
ключ для пункта: если пункт получает значимый положительный
фи-коэффициент, то ключ определяется значением «+1», если пункт
получает значимый отрицательный фи-коэффициент значением «-1».
Если пункт получает незначимый фи-коэфф.ициент, то его целесо-
образно исключить из теста.
При ручных вычислениях фи-коэффициента удобно вначале с
помощью формул (3.2.14) и (3.2.15) определить граничное значение
значимого (по модулю) фи-коэффициента. Например, при объеме
выборки в 100 человек и уровне значимости р < 0,01 пороговое зна-
чение вычисляется так:
27
.
0
100
63
,
6
2
01
,
0
n
x
(3.2.16)
При постоянном использовании компьютера при подсчете
суммарных баллов ключ для каждого пункта Q целесообразно опре-
делить в виде самого фи-коэффициента (или другого коэффициента
корреляции), определенного при коррелировании ответов на пункт с
суммарным баллом. Тогда тестовый балл подсчитывается по форму-
ле
k
j
j
ij
i
C
R
x
1
,
(3.2.17)
где х
i
— суммарный балл i-го испытуемого;
ij
R
-
ответ «верно» (+1) или «неверно» (-1) i-го испытуемого на
i-й пункт;
С
i
- ключ для i-го пункта: С = +1 для прямого, С= -1 для обрат-
ного.
Более чувствительный коэффициент, который также применя-
ется для дихотомических пунктов, - это точечный бисериальный ко-
эффициент корреляции, учитывающий амплитуду отклонения инди-
видуальных суммарных баллов от среднего балла:
i
i
x
i
n
pbi
q
p
S
x
p
x
n
r
*
1
3.2.18)
где
x* - сумма
финальных баллов тех индивидов, которые
дали утвердительный ответ на i-й пункт теста (решили i-ю задачу);

